Cinemática de un robot SCARA de 2 GDL.
Este programa pretende simular de forma simplificada la cinemática de un robot tipo SCARA de 2 grados de libertad. El objetivo es llevar la muñeca del robot de un punto a otro siguiendo una trayectoria rectilínea evitando sobreaceleraciones en las articulaciones.
Contents
Inicialización del programa.
clear all; clc Pi=[55;0]; % Coordenadas del punto inicial. Pf=[-30.77;-25.29]; % Coordenadas del punto final. time=1; % Tiempo en el que se tiene que realizar el movimiento.
Cálculo de los intervalos de tiempo entre una posición del robot y la siguiente. El número de posiciones es dado.
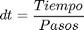
steps=20; dt=time/steps; t=0:dt:time;
Cinemática inversa.
La cinemática inversa consiste en determinar el ángulo que tienen que tomar las articulaciones del robot para seguir una determinada trayectoria.
En este caso, el robot tiene dos articulaciones que son:
- Giro del hombro
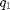
- Giro del codo
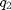
[x,y]=pathgen(Pi,Pf,time,steps); % La función pathgen nos devuelve los puntos (x,y) de la trayectoria rectilínea entre los puntos inicial y final.
q1=[];q2=[];
A continuación se utiliza la función inverse para obtener en 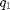 y
y 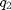 los sucesivos ángulos que tiene que tomar cada articulación para que el extremo del robot siga la trayectoria calculada.
los sucesivos ángulos que tiene que tomar cada articulación para que el extremo del robot siga la trayectoria calculada.
Los ángulos vienen dados por:
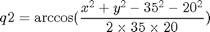
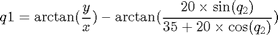
for i=1:1:numel(x) [q1(i),q2(i)]=inverse(x(i),y(i)); end
Interpolación en el espacio de los ángulos de la articulación.
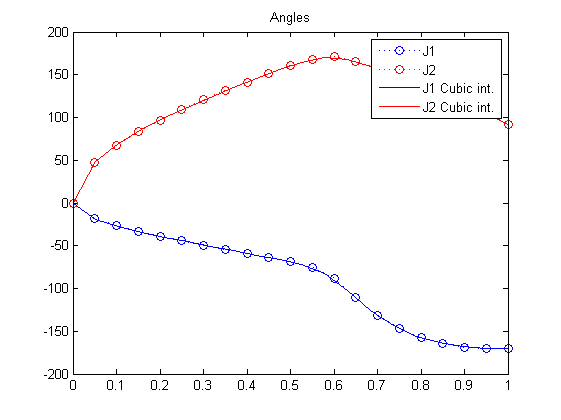
Para evitar discontinuidades entre posiciones angulares de las articulaciones (físicamente imposibles), se hace una interpolación mediante spline cúbica entre cada una de éstas posiciones.
xx = linspace(0,time,time*steps); spline1=csapi(t,q1,xx); spline2=csapi(t,q2,xx); figure,plot(t,q1*180/pi,'bo:'),hold on plot(t,q2*180/pi,'ro:') title('Angles') plot(xx,spline1*180/pi,'b-') plot(xx,spline2*180/pi,'r-') legend('J1','J2','J1 Cubic int.','J2 Cubic int.')
Cinemática directa.
La cinemática directa tiene en cuenta las dimensiones del robot y los ángulos relativos de las articulaciones para definir una matriz de transformación 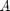 que permita conocer la posición del elemento final del robot.
que permita conocer la posición del elemento final del robot.
d1=32; d2=0; a1=35; a2=20; alfa1=0; alfa2=0; syms th th1 th2 a d alfa A=[cos(th) -sin(th)*cos(alfa) sin(th)*sin(alfa) a*cos(th) sin(th) cos(th)*cos(alfa) -cos(th)*sin(alfa) a*sin(th) 0 sin(alfa) cos(alfa) d 0 0 0 1]; A01=subs(A,[th d a alfa],[th1,d1,a1,alfa1]); % A01 es la matriz de transformación del elemento 0 (hombro) al elemento 1 (codo). clear A th th2 d a alfa % A12=subs(A,[th d a alfa],[th2,d2,a2,alfa2]); % T=A01*A12;
La matriz de transformación 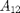 y total
y total 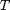 no son necesarias en este caso.
no son necesarias en este caso.
Representación gráfica del movimiento del robot.
n=100; h=figure; axis([-n,n,-n,n,0,n]); grid on ; hold on % Configuración de las dimensiones de la figura. p1=[0; 0; 0; 1]; p2=[0; 0; 32; 1]; p3=[35; 0; 32; 1]; p4=[55; 0; 32; 1]; pts=[p1 p2 p3 p4]; % Puntos de la estructura del robot. fix=plot3(x,y,ones(length(x))*32,'g'); % Dibujar trayectoria rectilínea. set(fix,'HandleVisibility','off') syms s Rz=[cos(s) -sin(s) 0 0;sin(s) cos(s) 0 0;0 0 1 0;0 0 0 1]; filename = 'animación-SCARA.gif'; for i=1:1:numel(spline1) %---Rotación del eje 1 (hombro)---- R1=double(subs(Rz,s,spline1(i))); ptsR1=pts; ptsR1=R1*ptsR1; %---Rotación del eje 2 (codo)---- R2=double(subs(Rz,s,spline2(i))); A01r=double(subs(A01,th1,spline1(i))); ptsR2=A01r\ptsR1; ptsR2=R2*ptsR2; ptsR2=A01r*ptsR2; cla plot3(ptsR1(1,1:3),ptsR1(2,1:3),ptsR1(3,1:3)) plot3(ptsR2(1,3:4),ptsR2(2,3:4),ptsR2(3,3:4),'r') drawnow % Guardar animación en un .GIF frame = getframe(h); im = frame2im(frame); [A,map] = rgb2ind(im,256); if i == 1; imwrite(A,map,filename,'gif','LoopCount',Inf,'DelayTime',0.1); else imwrite(A,map,filename,'gif','WriteMode','append','DelayTime',0.1); end end close all